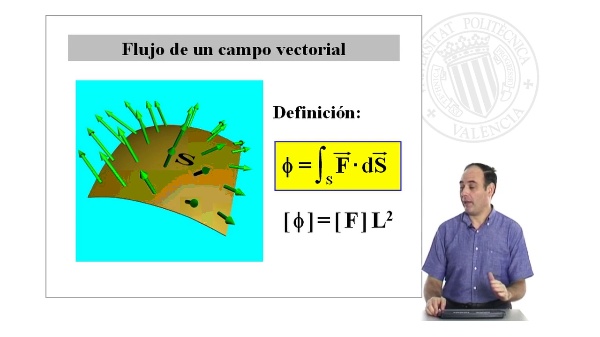
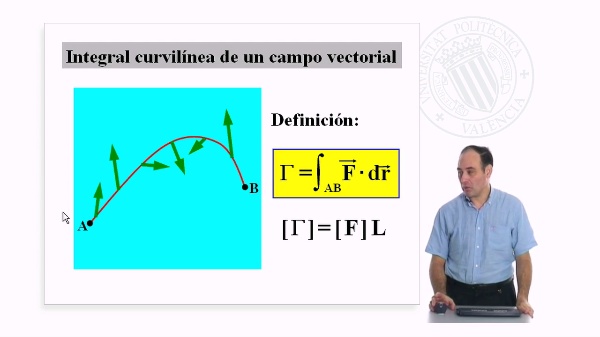
Derivadas direccionales de un campo escalar

En esta sesión calculamos las derivadas direccionales de un campo escalar real de dos variables. Partimos de la definición, como cociente de Newton, de derivada de una función real de una variable y generalizamos para el campo escalar para obtener las derivadas parciales. Vemos que la generalización es inmediata si consideramos las derivadas parciales como la derivada ordinaria respecto a una de las variables manteniendo la otra variable como constante. El significado geométrico de la defición de derivada parcial como la pendiente de la recta tangente al campo escalar en la dirección al eje de coordenada correspondiente a la variable de definición en el punto en el que se considere va a proporcionar la base para la generalización de estas derivadas parciales a las direccionales. Consideraremos una dirección, dada por un vector unitario, y veremos que la derivada direccional se corresponde con la pendiente de la recta tangente al campo escalar en el punto dado y la dirección considerada. Martínez Uso, MJ. (2018). Derivadas direccionales de un campo escalar. http://hdl.handle.net/10251/101945