Régimen estacionario de sistemas lineales (representación interna en variables de estado): constante/rampa/senoidal

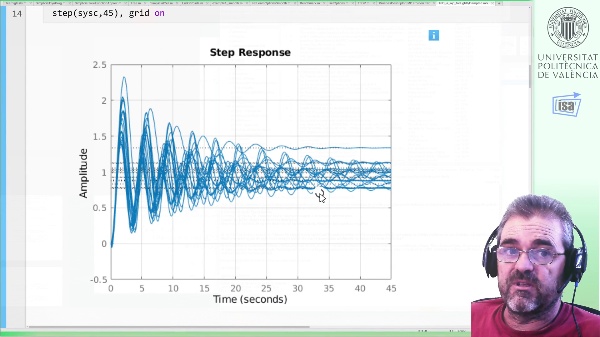
Este vídeo discute cómo calcular el régimen estacionario de sistemas en representación interna normalizada dx/dt=Ax+Bu, ante entradas constantes, rampa o senoidales. Las entradas constante/rampa/senoide se presentan como casos particulares de la salida de generadores lineales d(xi)/dt=M*xi, u=N*xi, marginalmente estables (valores propios de M en el eje imaginario). El componente transitorio se calcula a partir de M y N de forma aislada, sin calcular la respuesta temporal completa, mediante la resolución de una ecuación de Sylvester. Obviamente, el régimen estacionario ante una entrada constante es otro nombre para el concepto físico de ``punto de equilibrio'' 0=Ax_{eq}+Bu_{eq}, y el régimen estacionario ante una entrada senoidal es una reformulación del concepto de ``respuesta en frecuencia'' cuyo análisis en Función de Transferencia G(s) se aborda a partir de G(jw). La ecuación de Sylvester permite plantear estos problemas directamente en representación interna. Sala Piqueras, A. (2019). Régimen estacionario de sistemas lineales (representación interna en variables de estado): constante/rampa/senoidal. http://hdl.handle.net/10251/118001